You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Example 1:

Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: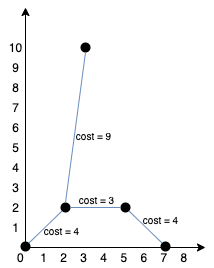
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
Example 2:
Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18
출처 :https://leetcode.com/problems/min-cost-to-connect-all-points/description/
풀이
function minCostConnectPoints(points: number[][]): number {
let minCost = 0;
let justAdded = points.shift() as number[];
const minCosts = new Map(points.map((point) => [point, Infinity]));
while (points.length) {
let nextMinCost = Infinity;
let minCostIndex = -1;
for (let i = 0; i < points.length; i++) {
const point = points[i];
const cost =
Math.abs(justAdded[0] - point[0]) + Math.abs(justAdded[1] - point[1]);
let minCostForPoint = minCosts.get(point)!;
if (cost < minCostForPoint) {
minCosts.set(point, cost);
minCostForPoint = cost;
}
if (minCostForPoint < nextMinCost) {
nextMinCost = minCostForPoint;
minCostIndex = i;
}
}
minCost += nextMinCost;
justAdded = points.splice(minCostIndex, 1)[0];
minCosts.delete(justAdded);
}
return minCost; // 총 최소 비용 반환
}
주어진 2차원 평면 상의 여러 포인트들을 최소 비용으로 연결하는 문제
예시 points = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
1. 초기 설정
let minCost = 0;
let justAdded = points.shift() as number[]; // 첫 번째 포인트 추출
const minCosts = new Map(points.map((point) => [point, Infinity])); // 포인트들에 대한 초기 비용 설정
- points.shift()로 첫 번째 포인트 [0, 0]을 추출해서 justAdded로 설정
- 남은 포인트들 [[2, 2], [3, 10], [5, 2], [7, 0]]에 대해 초기 비용을 Infinity로 설정
결과:
- justAdded = [0, 0]
- minCosts = { [2, 2]: Infinity, [3, 10]: Infinity, [5, 2]: Infinity, [7, 0]: Infinity }
2. 첫 번째 반복
while (points.length) {
let nextMinCost = Infinity;
let minCostIndex = -1;
for (let i = 0; i < points.length; i++) { // 남은 포인트들에 대해 거리 계산
const point = points[i];
const cost =
Math.abs(justAdded[0] - point[0]) + Math.abs(justAdded[1] - point[1]); // Manhattan 거리 계산
let minCostForPoint = minCosts.get(point)!;
if (cost < minCostForPoint) { // 더 작은 비용이면 갱신
minCosts.set(point, cost);
minCostForPoint = cost;
}
if (minCostForPoint < nextMinCost) { // 최소 비용 포인트 선택
nextMinCost = minCostForPoint;
minCostIndex = i;
}
}
첫 번째 while 반복이 시작되면, justAdded = [0, 0]이 기준점
포인트별 거리 계산:
- [0, 0]과 [2, 2] 사이의 거리: |0 - 2| + |0 - 2| = 4
- [0, 0]과 [3, 10] 사이의 거리: |0 - 3| + |0 - 10| = 13
- [0, 0]과 [5, 2] 사이의 거리: |0 - 5| + |0 - 2| = 7
- [0, 0]과 [7, 0] 사이의 거리: |0 - 7| + |0 - 0| = 7
minCosts = { [2, 2]: 4, [3, 10]: 13, [5, 2]: 7, [7, 0]: 7 }
가장 작은 비용은 4이고, 그에 해당하는 포인트는 [2, 2]
minCost += nextMinCost; // 최소 비용을 추가
justAdded = points.splice(minCostIndex, 1)[0]; // 최소 비용의 포인트 선택
minCosts.delete(justAdded); // 선택된 포인트 제거- minCost += 4로 minCost는 4가 됩니다.
- justAdded = points.splice(minCostIndex, 1)[0]로 [2, 2]을 선택하고 points에서 제거
- 이제 points = [[3, 10], [5, 2], [7, 0]].
결과:
- minCost = 4
- justAdded = [2, 2]
- points = [[3, 10], [5, 2], [7, 0]]
3. 두 번째 반복
두 번째 while 반복이 시작되면, justAdded = [2, 2]가 기준점
포인트별 거리 계산:
- [2, 2]과 [3, 10] 사이의 거리: |2 - 3| + |2 - 10| = 9
- [2, 2]과 [5, 2] 사이의 거리: |2 - 5| + |2 - 2| = 3
- [2, 2]과 [7, 0] 사이의 거리: |2 - 7| + |2 - 0| = 7
갱신된 minCosts:
minCosts = { [3, 10]: 9, [5, 2]: 3, [7, 0]: 7 }
가장 작은 비용은 3이고, 그에 해당하는 포인트는 [5, 2]
minCost += nextMinCost; // 최소 비용을 추가
justAdded = points.splice(minCostIndex, 1)[0]; // 최소 비용의 포인트 선택
minCosts.delete(justAdded); // 선택된 포인트 제거
- minCost += 3로 minCost는 7
- justAdded = points.splice(minCostIndex, 1)[0]로 [5, 2]을 선택하고 points에서 제거
- 이제 points = [[3, 10], [7, 0]].
결과:
- minCost = 7
- justAdded = [5, 2]
- points = [[3, 10], [7, 0]]
4. 세 번째 반복
세 번째 while 반복이 시작되면, justAdded = [5, 2]가 기준점
포인트별 거리 계산:
- [5, 2]과 [3, 10] 사이의 거리: |5 - 3| + |2 - 10| = 10
- [5, 2]과 [7, 0] 사이의 거리: |5 - 7| + |2 - 0| = 4
갱신된 minCosts:
minCosts = { [3, 10]: 9, [7, 0]: 4 }
가장 작은 비용은 4이고, 그에 해당하는 포인트는 [7, 0]
minCost += nextMinCost; // 최소 비용을 추가
justAdded = points.splice(minCostIndex, 1)[0]; // 최소 비용의 포인트 선택
minCosts.delete(justAdded); // 선택된 포인트 제거
- minCost += 4로 minCost는 11
- justAdded = points.splice(minCostIndex, 1)[0]로 [7, 0]을 선택하고 points에서 제거
- 이제 points = [[3, 10]].
결과:
- minCost = 11
- justAdded = [7, 0]
- points = [[3, 10]]
5. 네 번째 반복
네 번째 while 반복이 시작되면, justAdded = [7, 0]이 기준점
포인트별 거리 계산:
- [7, 0]과 [3, 10] 사이의 거리: |7 - 3| + |0 - 10| = 14
갱신된 minCosts:
minCosts = { [3, 10]: 9 }
가장 작은 비용은 9이고, 그에 해당하는 포인트는 [3, 10]
minCost += nextMinCost; // 최소 비용을 추가
justAdded = points.splice(minCostIndex, 1)[0]; // 최소 비용의 포인트 선택
minCosts.delete(justAdded); // 선택된 포인트 제거
- minCost += 9로 minCost는 20
- 이제 모든 포인트가 연결
결과:
- 최종 minCost = 20
최종 반환
최종 최소 비용 20을 반환
'LeetCode' 카테고리의 다른 글
| 1048. Longest String Chain / TypeScript (2) | 2024.09.10 |
|---|---|
| 2516. Take K of Each Character From Left and Right / TypeScript (0) | 2024.09.08 |
| CodeTestcaseTest ResultTest Result1410. HTML Entity Parser / TypeScript (1) | 2024.09.03 |
| 2166. Design Bitset / TypeScript (1) | 2024.09.01 |
| 2615. Sum of Distances / TypeScript (0) | 2024.08.25 |