Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:
- 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
- 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
- 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
- 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:

Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.
Example 2:
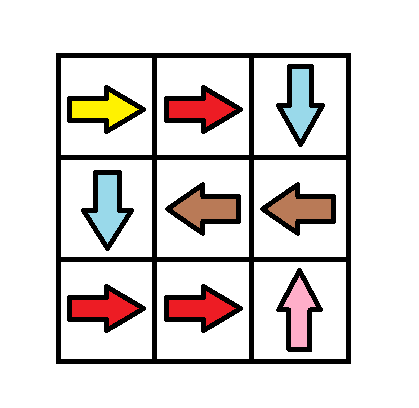
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:

Input: grid = [[1,2],[4,3]]
Output: 1
출처 : https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/description/
풀이
function minCost(grid: number[][]): number {
const m: number = grid.length;
const n: number = grid[0].length;
const checkPos = (i: number, j: number): boolean =>
i > -1 && j > -1 && i < m && j < n && !visited[i + "," + j];
const dir: { [key: number]: [number, number] } = {
1: [0, 1], // Right
2: [0, -1], // Left
3: [1, 0], // Down
4: [-1, 0], // Up
};
const dfs = (i: number, j: number): boolean => {
if (!checkPos(i, j)) return false;
if (i === m - 1 && j === n - 1) return true;
visited[i + "," + j] = true;
next.push([i, j]);
return dfs(i + dir[grid[i][j]][0], j + dir[grid[i][j]][1]);
};
const visited: { [key: string]: boolean } = {};
let changes: number = 0;
let cur: [number, number][] = [[0, 0]];
let next: [number, number][];
while (cur.length) {
next = [];
for (const [i, j] of cur) {
if (dfs(i, j)) return changes;
}
changes++;
cur = [];
next.forEach(pos => {
for (let d = 1; d < 5; d++) {
const x: number = pos[0] + dir[d][0];
const y: number = pos[1] + dir[d][1];
if (checkPos(x, y)) cur.push([x, y]);
}
});
}
}
2차원 배열에서 최소 비용으로 오른쪽 아래 끝까지 도달하는 경로를 찾는 문제를 해결하는 함수
문제 설명
주어진 grid는 m x n 크기의 2차원 배열로, 각 셀은 1에서 4까지의 숫자를 가짐.
각 숫자는 해당 위치에서 이동할 수 있는 방향을 나타냄.
- 1: 오른쪽으로 이동
- 2: 왼쪽으로 이동
- 3: 아래로 이동
- 4: 위로 이동
목표
시작점은 grid[0][0]이고, 도착점은 grid[m-1][n-1].
이 함수는 가능한 적은 비용으로 도착점에 도달하는 것
비용은 주어진 방향과 다른 방향으로 이동할 때 증가
코드 분석
- 변수 초기화:
- m: 그리드의 행 수
- n: 그리드의 열 수
- visited: 이미 방문한 위치를 저장하는 객체. 이 객체는 문자열로 좌표를 키로 저장하며, 방문했으면 true로 표시
- changes: 방향을 변경한 횟수. 비용을 추적하기 위해 사용
- cur: 현재 탐색할 위치를 저장하는 배열. 처음에는 시작점인 [0, 0]을 저장
- next: 다음 탐색할 위치를 저장하는 배열.
- 방향 정의:
- dir: 1, 2, 3, 4에 해당하는 각각의 이동 방향을 정의.
- 오른쪽, 왼쪽, 아래, 위로 이동하는 규칙을 {1: [0, 1], 2: [0, -1], 3: [1, 0], 4: [-1, 0]}로 정의
- 유효한 위치인지 확인하는 함수 checkPos:
- 이 함수는 주어진 좌표 (i, j)가 그리드 안에 있는지, 그리고 해당 위치를 이미 방문하지 않았는지를 확인
- 깊이 우선 탐색 함수 dfs:
- dfs 함수는 현재 위치에서 주어진 방향으로 이동하며 도착점에 도달하는지 확인
- 주어진 방향으로 이동하면서 방문하지 않은 위치가 있으면 계속해서 탐색을 진행
- 도착점에 도달하면 true를 반환
- 메인 로직:
- cur 배열에서 시작점 [0, 0]부터 탐색을 시작
- dfs 함수를 호출해 주어진 방향으로 이동하고, 만약 도착점에 도달하면 현재까지의 changes를 반환
- 도착하지 못하면 다음 단계로 넘어가면서 가능한 다른 방향으로 이동할 수 있는 위치를 next 배열에 저장
- changes를 증가시키고 다음 단계에서 탐색을 계속
코드 흐름
- 시작점에서 출발하여 주어진 방향으로 이동
- 이동할 때마다 방향을 변경하면 changes를 증가
- 도착점에 도달하면 그때까지의 방향 변경 횟수를 반환
- 도착할 수 없을 때까지 계속해서 탐색을 진행
예시 grid = [[1,1,1,1], [2,2,2,2], [1,1,1,1], [2,2,2,2]]
1. 그리드 설명
이 그리드는 4x4 크기로, 각 셀은 1에서 4까지의 값을 가짐. 각 값은 다음과 같은 방향을 나타냄
- 1: 오른쪽으로 이동
- 2: 왼쪽으로 이동
- 3: 아래로 이동
- 4: 위로 이동
즉, 이 그리드의 각 값은 이동할 수 있는 방향을 나타내고 있으며, 이동 방향이 다를 경우 비용(방향을 변경한 횟수)이 증가
[1, 1, 1, 1]
[2, 2, 2, 2]
[1, 1, 1, 1]
[2, 2, 2, 2]
2. 목표
출발점은 grid[0][0]이고, 도착점은 grid[3][3].
출발점에서 도착점까지 최소 비용(방향을 변경한 횟수)을 찾아야 함
3. 초기 상태
- cur 배열은 처음에 출발점인 [0, 0]을 포함
- visited 객체는 방문한 좌표를 저장
- 처음에는 아무 좌표도 방문하지 않음
- changes는 0으로 시작하며, 이 값은 방향을 바꿀 때마다 증가
4. 첫 번째 단계
- 현재 위치: [0, 0]
- 이 위치에서 이동할 수 있는 방향은 1이므로 오른쪽으로 이동. 즉, 다음 좌표는 [0, 1]
- dfs 함수가 호출되어 checkPos(0, 1)로 해당 위치가 유효한지 확인한 후, 계속해서 오른쪽으로 이동
- 이후 [0, 2]로 이동하고, 다시 [0, 3]로 이동
- 현재까지 방향을 변경하지 않았고, 계속 오른쪽으로 이동
이때 dfs는 주어진 방향으로 계속 이동하는데, 현재는 오른쪽으로만 이동했으므로 changes는 여전히 0
5. 두 번째 단계
- 현재 위치: [0, 3] (첫 번째 행의 마지막 칸)
- 더 오른쪽으로 갈 수 없으므로, 다음으로는 새로운 방향을 탐색
- 더 이상 오른쪽으로 이동할 수 없기 때문에 next 배열에 현재 위치 주변의 다른 방향으로 이동할 수 있는 위치들을 추가
이제 next에는 [0, 3]의 주변 위치가 추가되며, 다음과 같은 위치가 포함
- [1, 3]: 아래 방향으로 이동 (방향이 다르므로 비용 증가)
- [0, 2]: 왼쪽 방향으로 이동 (이미 방문한 위치)
이제 방향을 바꿔야 하므로 changes를 1 증가시키고, 아래로 이동.
그리드의 값에 따르면 아래 방향은 비용이 추가
6. 세 번째 단계
- 현재 위치: [1, 3]
- grid[1][3]의 값은 2로, 왼쪽으로 이동하는 방향을 나타냄. 따라서 이 지점에서 왼쪽으로 이동해야 함.
- 왼쪽으로 이동하여 [1, 2], [1, 1], [1, 0]으로 계속 이동
이 시점에서 방향 변경 없이 왼쪽으로 계속 이동했으므로 changes는 여전히 1
7. 네 번째 단계
- 현재 위치: [1, 0]
- 더 왼쪽으로 갈 수 없으므로 또 다른 방향을 탐색해야 함
- 다시 아래 방향으로 이동해야 하므로 next에 [2, 0]을 추가하고 방향을 변경하여 아래로 이동.
- 이때 changes는 2
8. 다섯 번째 단계
- 현재 위치: [2, 0]
- grid[2][0]의 값은 1로, 오른쪽으로 이동합니다. 따라서 이 위치에서 오른쪽으로 이동하여 [2, 1], [2, 2], [2, 3]으로 계속 이동
오른쪽으로 계속 이동했으므로 changes는 여전히 2
9. 여섯 번째 단계
- 현재 위치: [2, 3]
- 더 오른쪽으로 갈 수 없으므로, 또 다른 방향을 탐색해야 함
- 다시 아래 방향으로 이동하여 [3, 3]으로 이동.
- 이때 changes는 3.
10. 도착
- 현재 위치: [3, 3] (도착점)
- 도착점에 도달했으므로 최소 비용은 3
'LeetCode' 카테고리의 다른 글
| 2386. Find the K-Sum of an Array / TypeScript (0) | 2024.10.05 |
|---|---|
| 2301. Match Substring After Replacement / TypeScript (2) | 2024.09.29 |
| 736. Parse Lisp Expression / TypeScript (4) | 2024.09.24 |
| 2193. Minimum Number of Moves to Make Palindrome / TypeScipt (1) | 2024.09.23 |
| 1487. Making File Names Unique / TypeScript (1) | 2024.09.18 |